FoxCalculators - Libreng Mga Calculator Online!

Exponential decay / growth ay lubhang kapaki-pakinabang sa mathmatics. Ang pag-exponential decay ay nangyayari kapag ang rate ng paglago ay negatibo. Ang pagpaparami ng paglago sa parehong paraan ay nangyayari kapag ang rate ng paglago ng halaga ng isang matematikal na function ay proporsyonal sa kasalukuyang halaga ng function.

Ang formula para sa pagpaparami ng paglago ng isang variable x sa (positibo o negatibong) rate ng paglago R, bilang oras t napupunta sa discrete agwat (iyon ay, sa integer beses 0, 1, 2, 3, ...), ay < b> x _{t = x 0 (1 + r) ^{t .}}

Kung saan ang x _{0 ay ang halaga ng x sa oras 0. Kapag ang R ay negatibong ito exponential pagkabulok, kapag ang R ay positibo, ito ay exponential paglago. Halimbawa, ang rate ng paglago ng R = 5% = 0.05, mula sa anumang integer na halaga ng oras sa susunod na integer ay nagiging sanhi ng X sa pangalawang pagkakataon upang maging 1.05 beses kung ano ito sa nakaraang oras.}

Halimbawa, r = -0.5, ang graph ay bumababa (decaying). Ang bawat oras t ay nadagdagan ng 1, x _{t bumababa sa isang kalahati ng nakaraang halaga nito.}

Kapag r = 1, ang graph ay magiging paglago. Sa bawat oras na t ay nadagdagan ng 1, x _{t ay nagdaragdag sa pamamagitan ng isang kadahilanan ng 2.}

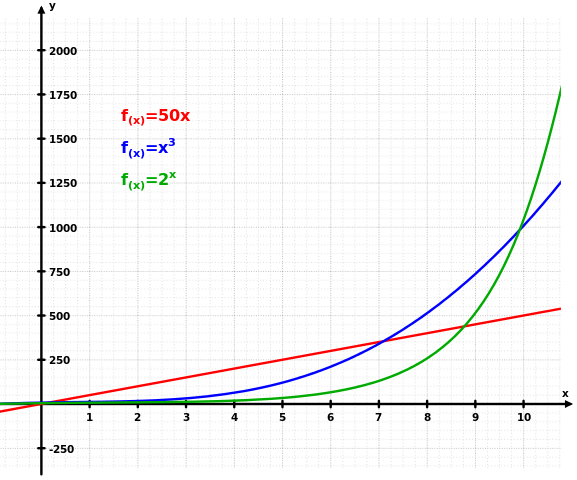
Ang graph ay nagpapakita kung paano ang pagpaparami ng paglago (berde) ay lumalampas sa parehong linear (pula) at kubiko (asul) paglago.